Nonlinear periodic optical structures are promising building blocks for functional, multi - wavelength photonic systems. With enhanced control, confinement, and manipulation of light waves, photonic bandgap structures provide new revolutionary horizonts for creating of parallel, all-optical computing and high-speed digital all-optical networking. The studies of nonlinear periodic optical structures focus on properties of new compact, modular and functional photonic devices.
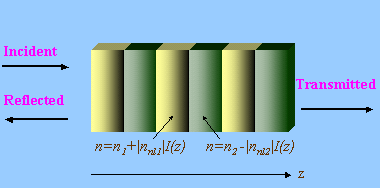Optical gratings can be manufactured from alternating bulk layers of
photonic crystals with different linear refractive indices and
different Kerr nonlinearities. Transmission of light through
the periodic material is simultaneously wavelength- and
intensity-dependent.
The periodic modulation of the linear refractive index induces a spectral gap in the material's bandwidth. The gap becomes wider with larger modulation depth (contrastness). The incident wave which wavelength fits inside the linear forbidden bandgap excites a resonant, strongly coupled counter-propagating wave. The resulting transmission is supported by the intensity-dependent refraction of the optical structure.
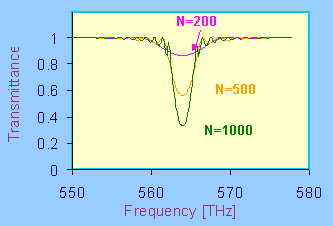The forbidden bandgap
is centered at a selected wavelength which satisfies the
condition for Bragg resonance between the light and
the optical material. The first bandgap occurs when
the light wavelength matches the double period of
the optical structure multiplied by the average
linear refractive index. It is the largest gap for
small modulation debth. There exist higher-order
bandgaps for smaller values of the light wavelength.
However, the higher-order bandgaps are narrow for small
modulation debth.
Mathematical modeling of optical gratings starts with the Maxwell equations, where the refractive index is periodic along the structure: n(z) = n0(z) + n2(z) I(z,t). Here I(z,t) is local intensity of light. Near the Bragg resonance, the electric field E(z,t) can be decomposed into two coupled modes for amplitudes of the forward (incident) wave A(z,t) and the backward (reflected) wave B(z,t):
E(z,t) = A(z,t) exp[i(kz - ωt)] + B(z,t) exp[-i(kz + ωt)]
In this approximation, the Maxwell equations can be reduced to a coupled-mode system. Basic types of the coupled-mode system are presented below for different physical approximations. Select the approximation on the left and check the type of the coupled-mode system on the right.
In the applet above, we have used the following notations:
| Derivatives: | A' = dA/dz + dA/dt; B' = dB/dz - dB/dt; |
| Parameters: | c - average of n0(z); d - average of n2(z); e - variance of n2(z). |
|
Guess what physical quantity conserved by the coupled-mode equations for time-independent light transmission through the periodic structure?! |
|
|
|
Transmission Regimes of Optical Gratings | |
|
|
Gap Solitons in Optical Gratings |