Transmission Regimes of Optical Gratings
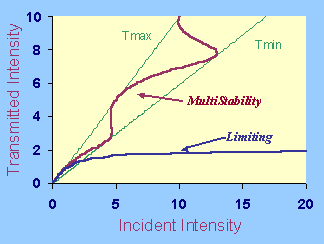
Intensity-dependent response of optical gratings is typically bistable
or multistable. At a given value of the incident intensity, stationary
light transmission is possible for two or more
values of the output intensity.
Optical bistability results in rapid transformation of the incident light
signal, as well as in hysteresis between states of low and high transmittance.
The input-output transmission curve has a remarkable S-shape
for the bistable transmission regime.
Bistable optical gratings are enabled by the periodic
modulation of the linear refractive index when the Kerr
nonlinearity is constant on average. At the contrary,
sufficiently strong compensation of the
nonlinear refractive index across different layers of
optical materials results in a uniform single-state
transmission of the periodic optical structure for
all ranges of the input intensity.
The transmitted intensity is clamped below the asymptotic
limiting value. Such nonlinear gratings are known as
optical limiters.
Dynamics of switching between different transmission states
in bistable optical gratings become complicated due to
development of side-band formations, leading to periodic
self-pulsations, and ultimately to the chaotic behaviour.
These phenomena limit the use of linear optical gratings
in photonic networks. At the contrary, the nonlinearity-compensated
optical limiters are uniformly stable with respect to
real-life disturbances. Such stable structures are
highly desirable for a number of
applications such as sensor and personnel protection,
all-optical signal processing, digital logic operations.
Here we show examples of optical devices
proposed on the basis of all-optical limiters. Select
the device on the left and check the picture on the right.
These devices can be mastered from photonic heterostructures such as
stacked slices of planar photonic crystals with different
linear and nonlinear refractive indices. The heterostructures
are designed to compensate the average Kerr nonlinearity and
to exhibit a counter-balance between linear refractive
properties and intensity-induced nonlinearity in each layer.
Such out-of-phase heterostructures display a two-step
response between zero and limiting intensities.
The two-step map is centered at a closing intensity,
when the nonlinearity-induced grating completely compensates
the linear grating. As a result, the out-of-phase grating
becomes transparent under incident light with the closing intensity.
However, the out-of-phase structures appear to be unstable for
non-zero average Kerr nonlinearities in longer devices.
Mathematical analysis of photonic heterostructures
and stationary and non-stationary transmission regimes
was performed on the basis of coupled-mode equations.
Details can be found in our recent papers:
|
|
D. Pelinovsky, L. Brzozowski,
and E.H. Sargent,
Transmission Regimes of Periodic
Nonlinear Optical Structures,
Phys. Rev. E 62, R4536-R4539 (2000)
|
|
|
|
D. Pelinovsky, J.Sears, L. Brzozowski,
and E.H. Sargent,
Stable All-optical Limiting
in Nonlinear Periodic Structures. I: Analysis,
J.Opt.Soc.Am.B 19, 43-53 (2002)
|
|
|
|
D. Pelinovsky and E.H. Sargent,
Stable All-optical Limiting
in Nonlinear Periodic Structures. II: Computations,
J.Opt.Soc.Am.B 19, 1873-1889 (2002)
|
New directions in this research are to model three-dimensional
photonic structures. Coupled-mode equations can be derived
for multiple-wave resonant configurations in the photonic crystals
under generalized (angle-dependent) Bragg resonance. Analysis
and modeling of such multiple-coupled-mode equations are yet
to be performed...
