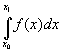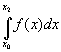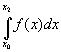CHAPTER 4: MATHEMATICAL MODELING WITH MATLAB

 

Lecture 4.2: Summation rules for numerical integration

 

Trapezoidal, Simpson and midpoint rules for integrals:

 

Problem: Given a set of data points:

(x0,y0); (x1,y1); (x2,y2); …(xn,yn)

Suppose the data points represent a function y = f(x). Suppose also that the data points are equally spaced with constant step size h = x1 - x0. Find a numerical approximation for the integral, which is the signed area under the curve y = f(x) between the end points (x0,y0) and (xn,yn).

 

Example: Linear electrical circuits can be easily miniaturized if they do not include large and bulky inductors. When a current I = I(t) is applied to the input port of a simple resistor-capacitor one-port network,  the voltage V = V(t) develops across the port terminals. At the time instance t = T, the voltage output is determined as a sum of the voltage drop across the resistor (which is R I(T)) and of the voltage drop across the capacitor (which is V0 + 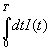/ C), where V0 is an initial voltage. If the input current I(t) can be measured at different times t = tk for k = 0,1,2,…,n, such that t0 = 0 and tn = T, them the integral is to be evaluated numerically from the given data set.

 

Solution: The function y = f(x) is either analytically defined or given in a tabular form. The numerical integration is based on the use of numerical interpolation y = Pn(x) fitted to the given data points and analytical integration of the polynomial Pn(x). This is a so-called Newton-Cotes integration algorithm. The most important Newton-Cotes integration formulas are trapezoidal, Simpson and midpoint rules.

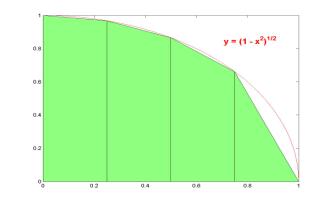
Trapezoidal rule:

 

A linear interpolation between the points (x0,y0) and (x1,y1) approximates the area under the curve y = f(x) by the area of the trapezoid:

   Itrapezoidal(f;x0,x1) = ( y1 + y0 )

Trapezoidal rule is popular in numerical integration as it is a simple method. Although its accuracy is low, the accuracy can be controled by doubling the number of elementary subintervals (trapezoids).

Simpson rule:

 

A quadratic interpolation between the points (x0,y0) (x1,y1), and (x2,y2) approximates the area under the curve y = f(x) by the area under the interpolant:

   ISimpson(f;x0,x2) = ( y0 + 4y1 + y2 )

Simpson rule is popular because of high accuracy of numerical integration compared to the trapezoidal rule.

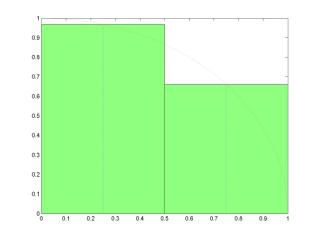
Mid-point rule:

 

A constant interpolation between the point (x1,y1), centered in the interval between (x0,y0) and (x2,y2), approximates the area under the curve y = f(x) by the area of a rectangle centered at the midpoint:

   Imid-point(f;x0,x2) = 2h y1

Mid-point rule is popular in numerical integration of functions with singularities at the end of the interval. It has the same accuracy as the trapezoidal rule and is often used in combination with the trapezoidal rule for computations of integrals near singularities.

 

h = 0.1; x0 = 0; x1 = x0+h; x2 = x0+2*h;

% the three data points are taken on [0,1] with equal step size

y0 = sqrt(1-x0^2); y1 = sqrt(1-x1^2); y2 = sqrt(1-x2^2);

yIexact = quad('sqrt(1-x.^2)',x0,x2); % 'exact answer' is computed by MATLAB

yItrap = h*(y0+y1+y1+y2)/2; % trapezoidal rule for two subintervals with h

yIsimp = h*(y0+4*y1+y2)/3;  % Simpson rule for two subintervals with h

yImid = 2*h*y1;  % mid-point rule for two subintervals with h

fprintf('Exact = %6.6f\nTrapezoidal = %6.6f\nSimpson = %6.6f\nMid-point = %6.6f',yIexact,yItrap,yIsimp,yImid);  

 

Exact = 0.198659

Trapezoidal = 0.198489

Simpson = 0.198658

Mid-point = 0.198997  

 

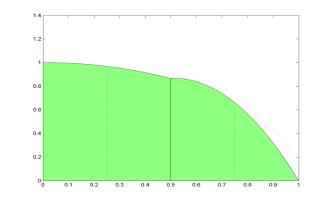
Composite summation rules:

 

The summation rules are extended to multiple intervals, when the function y = f(x) is represented by (n+1) data points with constant step size h. The composite rule is obtained by summating areas of all n individual areas.

 

·         Composite trapezoidal rule:

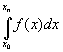
  Itrapezoidal(f;x0,x1,…,xn) = ( y0 + 2 y1  + 2 y2 + … + 2 yn-1 + yn )

·         Composite Simpson rule:

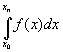
  Isimpson(f;x0,x1,…,xn) = ( y0 + 4 y1  + 2 y2 + 4 y3 + 2 y4 +  … + 2 yn-2 + 4 yn-1 + yn )

·         Composite mid-point rule:

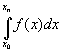
  Imid-point(f;x0,x1,…,xn) = 2h ( y1 + y3  + … + yn-3 + yn-1 )

For the composite Simpson and mid-point rules, the total interval between x [x0,xn] has to be divided into even number of subintervals.

 

Errors of numerical integration:

 

Numerical integration is much more reliable process compared to numerical differentiation. Rounding errors in computing sums in numerical integration are always constant, which are independent neither of the integration rule nor from the number of subintervals for summation. Truncation errors can be reduced with the use of more accurate summation rules for numerical integration.

 

Consider the equally spaced data points with constant step size: h = x2 – x1 = x1 –  x0. The theory based on the Taylor expansion method shows the following local truncation errors:

 

·         Trapezoidal rule:

f(x)dx – Itrapezoidal(f;x0,x1 ) = -f''(x),    x  [x0,x1]

The truncation error of the trapezoidal rule is proportional to h3, i.e. it has the order of O(h3). The error is also proportional to the second derivative of the function f(x) at an interior point x of the integration interval. Thus, the trapezoidal rule is exact for a linear function f(x).

 

·         Simpson rule:

f(x)dx – ISimpson(f;x0,x2 ) = -  f''''(x),    x  [x0,x2]

The truncation error of the Simpson rule is proportional to h5 rather than h3, i.e. it has the order of O(h5). The error is also proportional to the fourth derivative of the function f(x) at an interior point x of the integration interval. The Simpson rule is exact for polynomial functions f(x) of order m = 0,1,2,3.

 

·         Mid-point rule:

f(x)dx – Imid-point(f;x0,x2 ) =  f''(x),    x  [x0,x2]

The truncation error of the mid-point rule is as bad as that of the trapezoidal rule.

 

The global truncation error is computed for composite integration rules when an interval between x[x0,xn] is divided into n partial subintervals. The global truncation error is obtained by summation of local truncation errors and all local rounding errors:

 

·         Composite trapezoidal rule:

etrapezoidal =  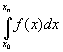|  - Itrapezoidal(f;x0,x1,…,xn) | <  M2 (xn – x0) + eps (xn – x0),

where M2 = max | f''(x)|. The global truncation error is proportional to the length of the integration interval and is order of O(h2).

 

·         Composite Simpson rule:

eSimpson =  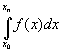|  - ISimpson(f;x0,x1,…,xn) | <  M4 (xn – x0) + eps (xn – x0),

where M4 = max | f''''(x)|. The global truncation error is proportional to the length of the integration interval and is order of O(h4).

 

h = 0.1; k = 1;

while (h > 0.0000001)

  x = 0 : h : 1; y = sqrt(1.-x.^2); n = length(x)-1;

  yIexact = pi/4; % exact integral, 1/4 of area of a unit disk

yItrap = h*(y(1)+2*sum(y(2:n))+y(n+1))/2; % composite trapezoidal rule

yIsimp = h*(y(1)+4*sum(y(2:2:n))+2*sum(y(3:2:n-1))+y(n+1))/3;

yImid = 2*h*sum(y(2:2:n));  % composite mid-point rule

eItrap(k) = abs(yItrap-yIexact); eIsimp(k) = abs(yIsimp-yIexact);

eImid(k) = abs(yImid-yIexact); hst(k) = h; h = h/2; k = k+1;

end,

plot(hst,eItrap,'g:',hst,eIsimp,'b--',hst,eImid,'r');

 

.

 

 

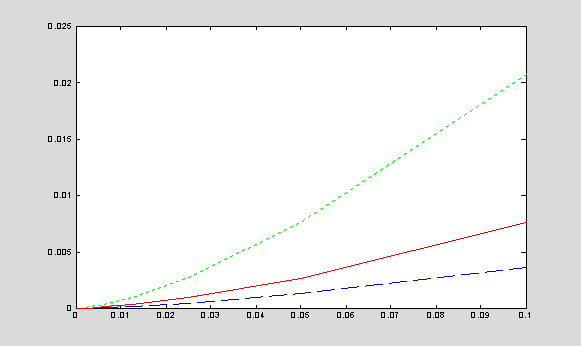
If the step size h between two points becomes smaller, the truncation error of the summation rule decreases. It decreases faster for Simpson rule and slower for trapezoidal and mid-point rule. For example, if h is halved, the global truncation error of the Simpson rule is reduced by a factor of 16, while the global truncation errors of the trapezoidal and mid-point rules are reduced only by a factor of 4.

 

Since the rounding error is bounded by the integration interval multiplied by the mashine precision eps, the error of numerical integration can be reduced to that constant global number.

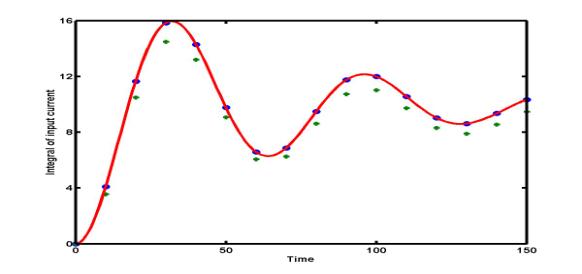
Example: The numerical approximations of the integral 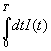, where I(t) is the current in a resistor-capacitor network, are obtained with step size h = 10 (green pluses) and with step size  h = 5 (blue dots), versus the exact  integral (red solid curve). The composite trapezoidal rule's error reduces with smaller step size h (blue dots are closer to the exact red curve compared to the green pluses). The figure also shows that the global truncation error for the integral grows with the length of the interval T.

 

MATLAB numerical integration:

 

·         quad: evaluates numerically the integral of a function by using adaptive Simpson quadrature

·         quadl: evaluates numerically the integral of a function by using adaptive Lobatto quadrature

·         dblquad: evaluates the double integral of a function of two variables in a rectangular domain

 

  % The function for numerical integration should be written as a MATLAB M-file

  % The functon should accept a vector argument X and return a vector result Y

  function [Y] = integrand(X)

     % this M-file sets up a function y = f(x) = sqrt(1 + exp(x))

     % which is the integrand for the integral to be evaluated by function "quad"

     Y = sqrt(1 + exp(X));

 

  % Compute the integral: I = int_0^2 sqrt(1 + exp(x)) dx

format long; I1 = quad(@integrand,0,2) 

% the default tolerance is 10^(-6) for absolute error of numerical integration

tolerance = 10^(-8); I2 = quad(@integrand,0,2,tolerance)

tolerance = 10^(-12); I3 = quad(@integrand,0,2,tolerance)

I4 = quadl(@integrand,0,2)

h = 0.0001; x = 0 : h : 2; y = feval(@integrand,x); n = length(y)-1;

I5 = h*(y(1)+2*sum(y(2:n))+y(n+1))/2 % composite trapezoidal rule

I6 = h*(y(1)+4*sum(y(2:2:n))+2*sum(y(3:2:n-1))+y(n+1))/3 % composite Simpson rule

I7 = 2*h*sum(y(2:2:n))  % composite mid-point rule  

I1 =  4.00699422404935

I2 =      4.00699422326706

I3 =   4.00699422325470

I4 =   4.00699422322700

I5 = 4.00699422402304

I6 =  4.00699422325470

I7 =   4.00699422171802  

 

W1 = quad('sin(pi*x.^2)',0,1), W2 = quad(inline('sin(pi*x.^2)'),0,1)

% standard MATLAB functions can be used for numerical integration as strings  

W1 =   0.5049

W2 =      0.5049  

Romberg integration for higher-order Newton-Cotes integration formulas:

 

More accurate integration formulas with smaller truncation error can be obtained by interpolating several data points with higher-order interpolating polynomials. For example, the third-order interpolating polynomial P3(x) between four data points leads to the Simpson 3/8 rule:

 

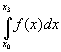
  ISimpson 3/8(f;x0,x3) = ( y0 + 3y1 + 3y2 + y3 )

 

while the fourth-order interpolating polynomial P4(x) between five data points leads to the Booles rule:

 

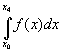
  IBooles(f;x0,x4) = ( 7 y0 + 32 y1 + 12 y2 + 32 y3  + 7 y4 )

 

The higher-order integration formulas can be recovered with the use of the Romberg integration algorithm based on the Richardson extrapolation algorithm.

 

·         Recursive integration formulas:

 

The composite trapezoidal rule has the global truncation error of order O(h2). Denote the composite trapezoidal rule for the integral of f(x) between [x0,xn] as R1(h). Compute two numerical approximations of the integral with two step sizes h and 2h:

f(x) dx = R1(h) + h2  ;          f(x) dx = R1(2h) + 4h4;

where  is unknown coefficient for the global truncation error. The number of trapezoids must be even in order the numerical approximation with double step-size (2h) could be computed. By cancelling the truncation error of order O(h2), we define a new integration rule for the same integral:

 

f(x) dx =  = R2(h)

 

The new integration rule R2(h) for the same integral is more accurate since the truncation error is of order O(h4). It is in fact the composite Simpson's rule as it can be checked directly. If the step size is sufficiently small, the composite Simpson's rule gives a much better numerical approximation for the integral, compared to the composite trapezoidal rule.

 

The process can be continued to find a higher-order integration formulas Rm(h) with the truncation error O(h2m). The recursive formula for Romberg integration formulas:

 

Rm+1(h) =Rm(h) +

 

 

 

 

·         Numerical algorithm

 

There are two modifications of the Romberg integration algorithm: with doubling the step size h and with halving the step size. The first modification is used when a limited number of data values is available. The second modification is more preferable if the function y = f(x) is available analytically and the data values (xk,yk) can be computed for any step size h. In order to compute the higher-order integration rules of the integral of f(x) between x0 x xn up to the order m, the number n must be matched with m as: n = 2m-1. In this case, there are sufficient number of points to compute integration rules of lower order with larger step sizes: h, 2h, 4h, 8h, …, (m-1)h. The numerical approximations for the integrals can be arranged in a table of recursive integration formulas starting with the simplest approximation R1(h) (composite trapezoidal rule):

 

step size

R1

R2

R3

R4

R5

h

R1(h)

 

 

 

 

2h

R1(2h)

R2(h)

 

 

 

4h

R1(4h)

R2(2h)

R3(h)

 

 

8h

R1(8h)

R2(4h)

R3(2h)

R4(h)

 

16h

R1(16h)

R2(8h)

R3(4h)

R4(2h)

R5(h)

 

The diagonal entries are values of higher-order integration rules for the integral of f(x) between x0 x xn . The higher-order approximation Rk(h) has the truncation error O(h2k). If h is small, the truncation error rapidly decreases with larger k. However, the rounding error is constant with larger value of k. As a result, no further increase in accuracy of numerical integration can be obtained after some number m M. The algorithm can be terminated when the relative error falls below an error tolerance.

 

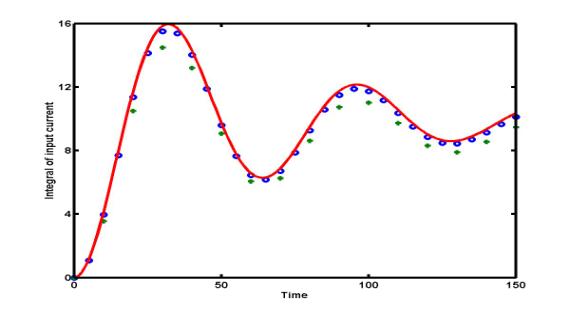
Example: The figure below presents the numerical approximations R1(h) and R2(h) for the integral of the current I(t) with the step size h = 10. Blue circles are found by the composite Simpson rule R2(h), green pluses are obtained by composite trapezoidal rule R1(h), and the exact integral of I(t) is shown by a red solid curve. The composite Simpson rule R2(h) is clearly more accurate than the composite trapezoidal rule R1(h).