CHAPTER 3: NUMERICAL ALGORITHMS WITH MATLAB
Lecture 3.4: Trigonometric
interpolation
General properties of trigonometric series:
Any
function y = f(x) that is
continuous and periodic function of x with period L can be replaced by
the trigonometric (Fourier) series (infinite sum of cosines and sines):
f(x) = ![]() a0 +
a0 + ![]() aj cos(2
aj cos(2![]() jx/L) + bj sin(2
jx/L) + bj sin(2![]() jx/L), 0
jx/L), 0 ![]() x
x ![]() L
L
where
(aj,bj) are Fourier coefficients computed
from the function f(x) by means of integrals:
aj = ![]()
![]() f(x) cos(2
f(x) cos(2![]() jx/L) dx, j =
0,1,2,…,
jx/L) dx, j =
0,1,2,…,![]()
and
bj = ![]()
![]() f(x) sin(2
f(x) sin(2![]() jx/L) dx, j =
1,2,…,
jx/L) dx, j =
1,2,…,![]()
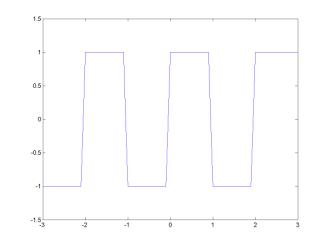
Example: f(x) = sign(x), -1 < x < 1 ; f(x + 2) = f(x), L = 2.
|
|
Trigonometric series for sign-function: f(x) = |
Trigonometric interpolation:
Problem: Given a set of (n+1)
data points:
(x1,y1);
(x2,y2); …; (xn,yn); (xn+1,yn+1)
,
such
that the values of x are equally spaced on the interval x ![]() [0,L] and the
values of y are periodic with period of L, i.e. yn+1
= y1. Find a finite sum of cosines and sines y =
f(x) that connects all (n+1) data points.
[0,L] and the
values of y are periodic with period of L, i.e. yn+1
= y1. Find a finite sum of cosines and sines y =
f(x) that connects all (n+1) data points.
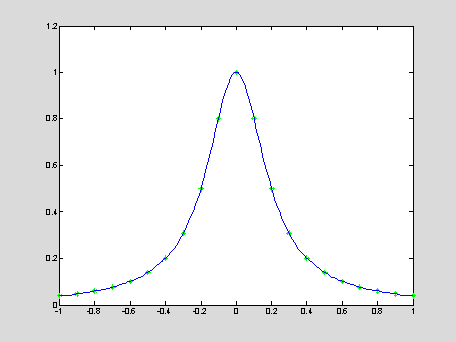
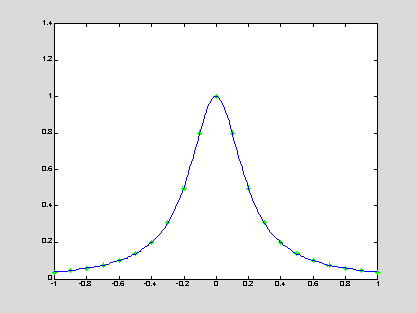
Example:
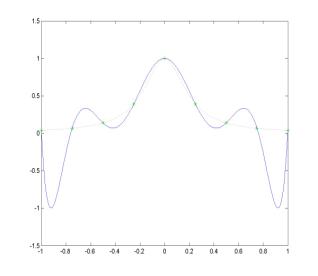
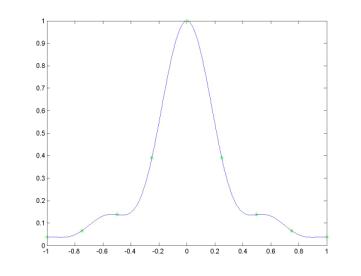
Consider
interpolation of the Runge function y = 1/(1 + 25 x2). The
polynomial interpolation (on the left) does not produce any good approximation
of the Runge function because of the polynomial wiggle. The trigonometric
interpolation (on the right) reproduces the Runge function on the interval -1
< x < 1 with sufficiently small error.
|
|
|
Methods:
·
Linear
systems for Fourier coefficients
·
Summation
formulas for Fourier coefficients
·
Discrete
Fourier Tranform
Linear systems for Fourier coefficients:
The
interval x ![]() [0,L] has the
equally-spaced partition at the values of x:
[0,L] has the
equally-spaced partition at the values of x:
xi =
(i-1)L/n, i=1,2,…,n
The
trigonometric interpolation y = f(x) should have n coefficients
[aj,bj], which are to be found from n
equations: yi = f(xi). If n is
even, i.e. n = 2m, the trigonometric interpolant y = f(x) takes
the form:
f(x) = ![]() a0 +
a0 + ![]()
![]() aj cos(2
aj cos(2![]() jx/L) + bj sin(2
jx/L) + bj sin(2![]() jx/L)
jx/L) ![]() + am cos(2
+ am cos(2![]() mx/L)
mx/L)
The
Fourier coefficients are to be found from the linear system:
yi = ![]() a0 +
a0 + ![]()
![]() aj cos(2
aj cos(2![]() j xi / L) + bj sin(2
j xi / L) + bj sin(2![]() j xi / L)
j xi / L)![]() + am cos(2
+ am cos(2![]() mxi/L)
mxi/L)
x = -1
: 0.1 : 1; % equally-spaced partition of the interval: –1 < x < 1
y = 1./(1 + 25*x.^2); % values of the Runge function
n = length(x)-1; m = n/2; L = 2;
xx = [x(m+1:n),x(1:m)]'; yy = [y(m+1:n),y(1:m)]';
% continuation of data to
the positive interval for x in [0,L]
A = 0.5*ones(n,1); % building the coefficient matrix for linear
system
for j = 1 : (m-1)
A = [ A,
cos(2*pi*j*xx/L), sin(2*pi*j*xx/L) ];
end
A = [ A, cos(2*pi*m*xx/L) ];
c = A\yy; % computations of Fourier coefficients in a special
order
a = [ c(1); c(2:2:n) ]; b = [0; c(3:2:n)]; % coefficients are
column vectors
a',b', xInt = -1: 0.01 : 1; % interpolation partition on the same
interval
yInt = 0.5*a(1)*ones(1,length(xInt));
for j = 1 : (m-1)
yInt = yInt +
a(1+j)*cos(2*pi*j*xInt/L) + b(1+j)*sin(2*pi*j*xInt/L);
end
yInt = yInt + a(m+1)*cos(2*pi*m*xInt/L);
ans = 0.5492
0.3442 0.1756 0.0970
0.0499 0.0279 0.0140
0.0084 0.0041 0.0032
0.0010
ans = 1.0e-016 *
0.1228 0.1459 0.0789
0.0692 0.0106 -0.3902
0.1272 0.1426 0.0627
Summation
formulas for Fourier coefficients:
When
the partition of the interval x ![]() [0,L] is equally spaced, the Fourier coefficients [aj,bj]
can be computed from direct summation formulas:
[0,L] is equally spaced, the Fourier coefficients [aj,bj]
can be computed from direct summation formulas:
aj = ![]()
![]() yi cos(2
yi cos(2![]() jxi /L),
j = 0,1,2,…,m
jxi /L),
j = 0,1,2,…,m
and
bj = ![]()
![]() yi sin(2
yi sin(2![]() jxi / L),
j = 1,2,…,m-1
jxi / L),
j = 1,2,…,m-1
These
formulas represent the discrete Fourier transform defined at the given set of
data points (xi,yi).
P = A'*A; % summation formulas follows from
the fact that A'*A is diagonal
P(1:6,1:6)
% the discrete cosines and sines are orthogonal with respect to sums!
5.0000
0.0000 -0.0000 0.0000
-0.0000 0.0000
0.0000
10.0000 -0.0000 0.0000 0 -0.0000
-0.0000
-0.0000 10.0000 -0.0000
-0.0000 0.0000
0.0000
0.0000 -0.0000 10.0000
0.0000 0.0000
-0.0000 0 -0.0000 0.0000
10.0000 -0.0000
0.0000 -0.0000 0.0000 0.0000 -0.0000 10.0000
x = -1 : 0.1
: 1; y = 1./(1 + 25*x.^2);
n = length(x)-1; m = n/2; L = 2;
xx = [x(m+1:n),x(1:m)]'; yy = [y(m+1:n),y(1:m)]';
for j = 0 : m
a(j+1) = 2*yy'*cos(2*pi*j*xx/L)/n;
b(j+1) = 2*yy'*sin(2*pi*j*xx/L)/n;
% inner (dot) product is used for computations
% b(1) = b(m+1) = 0
end
a',b', xInt = -1: 0.01 : 1;
yInt = 0.5*a(1)*ones(1,length(xInt));
for j = 1 : (m-1)
yInt = yInt + a(1+j)*cos(2*pi*j*xInt/L)
+ b(1+j)*sin(2*pi*j*xInt/L);
end
yInt = yInt + a(m+1)*cos(2*pi*m*xInt/L);
plot(x,y,'*g',xInt,yInt,'b');
ans = 0.5492 0.3442
0.1756 0.0970 0.0499
0.0279 0.0140 0.0084
0.0041 0.0032 0.0020
ans = 1.0e-016 *
0 -0.0833 -0.2220 0 0.1110 0
0.1110 -0.1110 0.0555
-0.0278 0.0471
Discrete
Fourier Transform:
The trigonometric sum can be rewritten as a complex Fourier sum:
f(x) = ![]()
![]() cj exp( 2
cj exp( 2![]() i*
i*![]() ), i =
), i = ![]() , 0
, 0 ![]() x
x ![]() L (1)
L (1)
where cj = n (aj - ibj)
/ 2 and
c-j = n (aj + ibj ) / 2. The complex
Fourier coefficients cj are found from the summation
formulas:
cj = ![]() yk exp(-2
yk exp(-2![]() i*
i*![]() ), j = 0,
), j = 0,![]()
![]() ,…,
,…,![]() (2)
(2)
Given
data points (xk,yk) for k = 1,…,n and
n = 2m, formulas (2) are usually referred to as the discrete Fourier
transform (DFT), while formulas (1) at the points (xk,yk)
are referred to as the inverse discrete Fourier transform (IDFT). We
use a simple observation:
c-j = exp(2![]() i*
i*![]() ) = exp(2
) = exp(2![]() i*
i*![]() ) = exp(2
) = exp(2![]() i*
i*![]() ) = cn-j
) = cn-j
Then,
the discrete and inverse discrete Fourier transforms can be regrouped for
positive indices:
cj = ![]() yk exp(-2
yk exp(-2![]() i*
i*![]() ), j = 0,1,2,…,n-1
), j = 0,1,2,…,n-1
and
yk = ![]()
![]() cj exp( 2
cj exp( 2![]() i*
i*![]() ).
).
These
formulas are valid only at the discrete data points (xk,yk).
In order to actually interpolate the function y = f(x) beyond
the data points (xk,yk), we would need to
use the formula for trigonometric interpolation with:
aj = ![]() Re(cj);
bj = -
Re(cj);
bj = -![]() Im(cj);
j = 0,1,…,m,
Im(cj);
j = 0,1,…,m,
where
m = n/2.
·
fft: computes
the discrete Fourier transform
·
ifft: computes
the inverse discrete Fourier transform
x = -1 : 0.5
: 1; y = 1./(1 + 25*x.^2); % data points
n = length(x)-1; m = n/2; L = 2;
xx = [x(m+1:n),x(1:m)]'; yy = [y(m+1:n),y(1:m)], yy = yy';
for j = 0 : m
a(j+1) = 2*yy'*cos(2*pi*j*xx/L)/n;
b(j+1) = 2*yy'*sin(2*pi*j*xx/L)/n;
end
a =a, b =b % Fourier
coefficients of trigonometric series
c = fft(yy); c = c'
aF = 2*real(c(1:m+1))/n; bF = -2*imag(c(1:m+1))/n;
aF = aF, bF = bF % Fourier
coefficients derived from FFT
yF = ifft(c) % the same
function y is recovered, i.e. yF = ifft(fft(y)) = y
yy = 1.0000 0.1379
0.0385 0.1379
a = 0.6572 0.4808 0.3813
b = 1.0e-017 *
0 0
0.4710
c = 1.3143 0.9615
0.7626 0.9615
aF = 0.6572 0.4808
0.3813
bF = 0 0
0
yF = 1.0000 0.1379 0.0385 0.1379
In
order to compute the function y = f(x) at data points different
from (xk,yk), the trigonometric sum should
be used:
f(x) = ![]() a0 +
a0 + ![]()
![]() aj cos(2
aj cos(2![]() jx/L) + bj sin(2
jx/L) + bj sin(2![]() jx/L)
jx/L) ![]() + am cos(2
+ am cos(2![]() mx/L)
mx/L)
Trigonometric
approximation:
If m
< n/2, the trigonometric sum only approximates the function y
= f(x) in the least-square sense, since there are more data points (xk,yk)
than the Fourier coefficients (aj,bj)
to be found.
·
fft(y,N), ifft(y,N): compute the trigonometric interpolation if N =
length(y), the trigonometric approximation if N < length(y) and
the trigonometric interpolation with padded zeros for y if
N > length(y)
x = 0 : 0.01
: 1; y = x.*(1-x); % data points
n = length(x)-1; m = n/2; L = 1;
xx = x(1:n)'; yy = y(1:n)';
N = 10; mN = N/2; c = fft(yy,N);
a = 2*real(c(1:mN+1))/N; b = -2*imag(c(1:mN+1))/N;
aa = a', bb = b'
xInt = 0: 0.01 : 1; yInt = 0.5*a(1)*ones(1,length(xInt));
for j = 1 : (mN-1)
yInt = yInt +
a(1+j)*cos(2*pi*j*xInt/L) + b(1+j)*sin(2*pi*j*xInt/L);
end
yInt = yInt + a(mN+1)*cos(2*pi*mN*xInt/L);
plot(x,y,'*g',xInt,yInt,'b');
aa = 0.0843 -0.0100
-0.0093 -0.0092 -0.0091
-0.0091
bb = 0 -0.0277
-0.0124 -0.0065 -0.0029 0
|
|
|
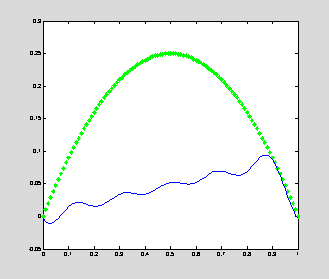
The
trigonometric approximation with N = 10 is shown on the left.
The
trigonometric interpolation with N = n = 100 is shown on the
right.