CHAPTER 1: INTRODUCTION INTO MATLAB COMPUTING

Lecture 1.6: Errors of MATLAB numerical computations

Types of errors:

· rounding errors (due to finite precision arithmetic)

· truncation errors (due to discretization and truncation of series)

· experimental errors (due to inaccuracy in data values)

Definitions of errors:

Suppose: x_ex - exact value of x; x_ap – approximate (computer) value of x.

· Absolute error: E_abs = | x_ap - x_ex |

· Relative error: E_rel = | x_ap - x_ex | / | x_ex |

E_rel ~ 10^-4, | x_ex | ~ 1, then x_ap has an error in the fourth digit after the period

E_rel ~ 10^-4, | x_ex | ~ 10^-5, then x_ap has an error in the ninth digit after the period

E_rel ~ 10^-4, | x_ex | ~ 10⁵, then x_ap has an error in the first digit before the period

Truncation versus rounding errors:

Computer may represent only finite-sum or finite-difference approximations. Therefore, the computer representations always have a truncation error. Adding more terms to the finite-sum or finite-sum approximations may decrease the truncation error if the convergence is uniform. However, the convergence is not improved after the truncation error becomes comparable with the rounding error, produced by floating point arithmetic. Numerical computations always rely on an inexact computer arithmetic system.

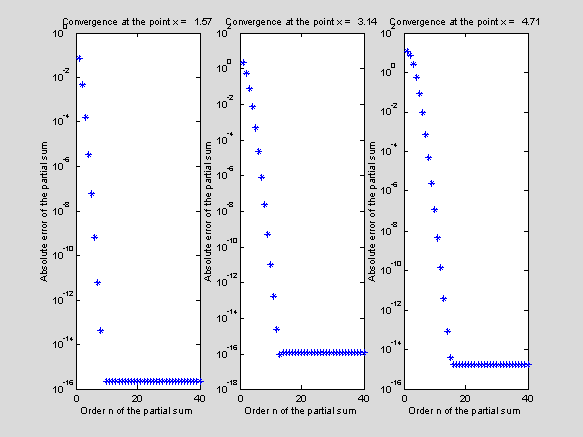
% Taylor series for y = sin(x):

% sin(x) = (-1)^n*x^(2n+1) / (2n+1)! = x – x^3/3! + x^5/5 - …

% The Taylor series converges to y = sin(x) for any |x| < inf

% Computations of sin(x) for n-finite partial sums:

x = [pi/2,pi,3*pi/2];

S = x; Term = S;

y_ex = sin(x);

for n = 1 : 40

Term = -Term.*x.*x/(2*n*(2*n+1));

S = S + Term;

E_abs(n,:) = abs(S-y_ex);

end

for k = 1:length(x)

subplot(1,length(x),k);

semilogy(E_abs(:,k),'*');

xlabel('Order n of the partial sum');

ylabel('Absolute error of the partial sum');

title(sprintf('Convergence at the point x = %5.2f',x(k)));

end

MATLAB errors:

· realmin: smallest positive floating point number

· realmax: largest positive floating point number

realmin, realmax

% MATLAB gives wider range of numbers compared to double precision on a standard workstation

ans =

2.2251e-308

ans =

1.7977e+308

· eps: mashine precision, the distance from 1.0 to the next floating point value greater than 1.0; the computer system cannot express any value between [1,1+eps] and it rounds the value to 1 or 1+eps

· 0.5*eps: maximum relative rounding error associated with the floating point arithmetic

eps % MATLAB precision is about the same as the double precision on a typical workstation

ans =

2.2204e-016

Examples of rounding errors:

Rounding errors attend every floating point arithmetic operation, such as addition, subtraction, multiplication, and division.

· floating point underflow (x_min is the mashine zero: if 0 <= x < x_min, then x = 0 )

x = 1; q = 0;

while ( x ~= 0 )

x = x/2;

q = q + 1;

end

q % the power for the smallest positive number, when 1 / 2^q = 0

xMin = 1 / 2^q % mashine zero in floating point arithmetic

q = 1075

xMin = 0

· floating point overflow (x_max is the mashine infinity: if x > x_max, then x = inf )

x = 1; q = 0;

while ( x ~= inf )

x = 2*x;

q = q + 1;

end

q % the power for the largest positive number, when 2^q = inf

xMax = 2^q % mashine infinity

x1 = 1/inf % it must be zero

x2 = i*inf % it does not have sense, i.e. NaN

q = 1024

xMax = Inf

x1 = 0

x2 = NaN + Infi

· floating point precision ( eps is the mashine precision: if 1 < x < 1 + eps, then x = 1 )

x = 1; q = 0; y = 1; z = x + y;

while ( x ~= z )

y = y/2;

q = q + 1;

z = x + y;

end

q % the power for the smallest positive number, when 1 + 1 / 2^q = 1

xEps = 1 + 1 / 2^q % it must be one

q = 53

xEps = 1