Nonlinear Damped Pendulum

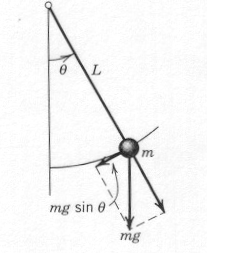
Any object that swings back and forth is called a physical pendulum. The nonlinear pendulum consists of a rod of length l, to which a mass m is attached at one end:

The mathematical model for pendulum is derived from the Newton's second law: F = m a, where F = - mg sinθ is the tangential component of the gravity force and a = l θ'' is the angular acceleration. The displacement angle θ is measured counterclockwise from the vertical axis. The mathematical model for pendulum takes the form:

Notice that the motion of pendulum does not depend on its mass m. The gravity acceleration is constant: g = 9.8 (m/s²).

If the pendulum is placed into viscous medium, such as water or smoked air, the viscous friction needs to be taken into account. The viscous friction modifies the mathematical model for pendulum by the damping term, proportional to the angular velocity:

where k is the coefficient of friction: k > 0. The software simulator models dynamics of the nonlinear damped pendulum for different values of k and l and for different initial values of the displacement angle θ and the angular velocity θ'.

It is clear from physics that the pendulum rests in equilibrium in the vertical position, where θ = 0, as well as in the inverted vertical position, where θ = π. The vertical position θ = 0 is clearly stable, since a small initial displacement of the pendulum results in its swinging around the equilibrium. The inverted vertical position θ = π is clearly unstable, since a small initial displacement of the pendulum results in its bouncing down.

On the language of dynamical systems and phase planes, the two equilibrium positions are critical points of the model. The critical point at θ = 0 is locally stable: it is a center point for k = 0 a stable spiral point for 0 < k < 2 (gl)^1/2, and a stable node for k > 2 (gl)^1/2. The critical point at θ = π is locally unstable: it is a saddle point for any k >= 0.

In the undamped case, when k = 0, possible dynamical regimes of the pendulum can be classified from possible trajectories shown on the phase plane:

If the pendulum is slightly pushed near θ = 0, it will be swinging back and forth around the vertical equilibrium. Effective solutions for the oscillating pendulum are periodic in time. Such periodic solutions are described by the finite trajectories on the phase plane.

However, if the pendulum is pushed hard enough, it will be spining in complete circles about its pivot. The displacement angle θ = θ(t) only increases or descreases for the rotating pendulum. Therefore, effective solutions are non-periodic in time. They are described by infinite trajectories on the phase plane.

The finite (periodic) and infinite (non-periodic) solutions are separated by special trajectories called the separatrix curve. The separatrix curves describe special moves of the pendulum: it starts in the unstable inverted vertical position, makes a complete spin about its pivot, and returns to the inverted vertical position. The pendulum makes only one loop for the whole time interval. Separatrix curves separate two qualitatively different dynamical regimes of the pendulum on the phase plane: periodic oscillations and non-periodic rotations.

When the pendulum is placed into viscous medium, when k > 0, possible dynamical regimes of the pendulum are seen from the new phase plane:

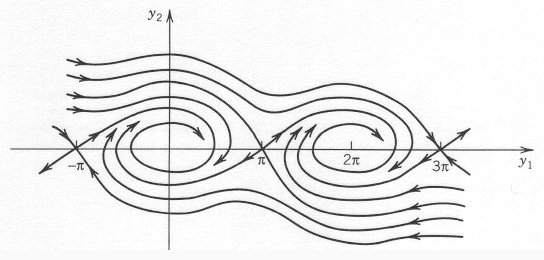
In the damped case, all closed trajectories for periodic solutions are destroyed, and the trajectories spiral around one of the critical points, corresponding to the vertical equilibrium of the pendulum. On the phase plane, these critical points are stable spiral points for the underdamped pendulum (when k < 2 (gl)^1/2), and they are stable nodes for the overdamped pendulum (when k > 2 (gl)^1/2). The unstable equilibrium at the inverted vertical position remains an unstable saddle point. It is clear physically that damping means loss of energy. The dynamical motion of the pendulum decays due to the friction and the pendulum relaxes to the equilibrium state in the vertical position.

You are suggested to check the physical conclusions above by running numerical simulations of the pendulum software demo. It is recommended to attend the following questions in your simulations:

1. Consider the undamped case: k = 0 and set the initial angular velocity θ' to zero. Increase initial angle θ in the following order: θ = 45,90,135,180. What type of dynamics do you see? Are trajectories finite or infinite? Is the motion of pendulum periodic or non-periodic?
   
   
2. Change the initial angular velocity: θ' = 50 (i.e. you push the pendulum up). Increase the initial angle in the same order: θ = 45,90,135,180. Do you identify two different types of dynamics? Check if your initial point lies inside or outside of the separatrix curve.
   
   
3. Consider the damped case: k = 1 and repeat simulations in (1) and (2). Observe that, no matter what your initial point is, the pendulum always results in the stable vertical position: θ = 0.
   
   
4. Set k = 0 and initial values as θ = 45 and θ' = 0. Change the length of the pendulum in the following order: l = 7,10,13. Do you observe any changes in the period of oscillations? Any changes in the size of the separatrix curve? Any changes in trajectories on the phase plane?